2020 Volume 3 Issue 2

Modern equipment requires the creation of multifunctional, and in the future, even hyperfunctional materials, which can be developed only as multicomponent systems. One of the ways of addressing this challenge is based on the use of different fillers in polymer compositions. A broad spectrum of fillers and a possibility of combining the particles having different natures, shapes, and sizes enable directed modification of the operational characteristics of polymer composites, with mechanical properties of the composite materials being determining irrespective of their functional assignment [1–8].

Traditionally, a basis for optimizing the properties of composite polymeric materials of the so-called large-scale production was an empirical search for the best combination of properties of the initial components and phase morphology of the final product [5–9]. However, modern materials science of polymers requires more detailed information on the factors that determine the operational properties of the composites and the mechanisms that are responsible for their deformation behavior in a wide range of strains up to the ultimate values.

The goal of the present work was to study the mechanical properties of the composites based on polyethylene and determine the effect of temperature on their deformation behavior and fracture.

Results and discussion

Figure 1 shows the stress–strain curves of unfilled HDPE at different temperatures. The character of polymer deformation does not depend on the test temperature. Both at 20 °C and at the elevated temperatures, the uniaxial tension results in the formation of a neck and fracture of the polymer during propagation of the neck through a gauge section of the sample. In this case, the tensile strength of HDPE is equal to the necking stress (draw stress). It should be noted that at 20 and 30 °C the sample fracture occurs at a boundary of the growing neck, while at 70–90 °C it proceeds in the center of the neck once a certain draw ratio is achieved.

Figure 1. Stress–strain curves of initial HDPE (a) and the composites on its base bearing 3 (b) and 10 (c) vol % of the filler.
The test temperatures were as follows: 20 (1), 30 (2), 50 (3), 70 (4), and 90 (5) °C.

Table 1 lists the mechanical properties of HDPE at different temperatures. The upper yield stress σ_y and the tensile strength σ_m and height of a yield peak (σ_y–σ_m) of HDPE reduce with a temperature rise (Т). The relative elongation at break of the polymer firstly increases, and then, at Т > 50 °C, reduces due to the propensity of HDPE for high-temperature embrittlement [10].

Table 1. HDPE properties at different temperatures^a

Figure 2 shows the dependences of the neck draw ratio of HDPE λ_d on the tensile strain at different temperatures. Of note are unusually high values of λ_d. Moreover, the value of λ_d of the polymer is not constant and increases with neck propagation. At T > 20 °C, the rate of λ_d variation increases. Thus, at 70 °C, λ_d is equal to 8.5 at the tensile strain of 100%, while at ε = 400% it reaches 24. The variability of λ_d evidences the occurrence of two simultaneous processes during HDPE deformation, namely, the neck propagation and polymer creep at the neck.

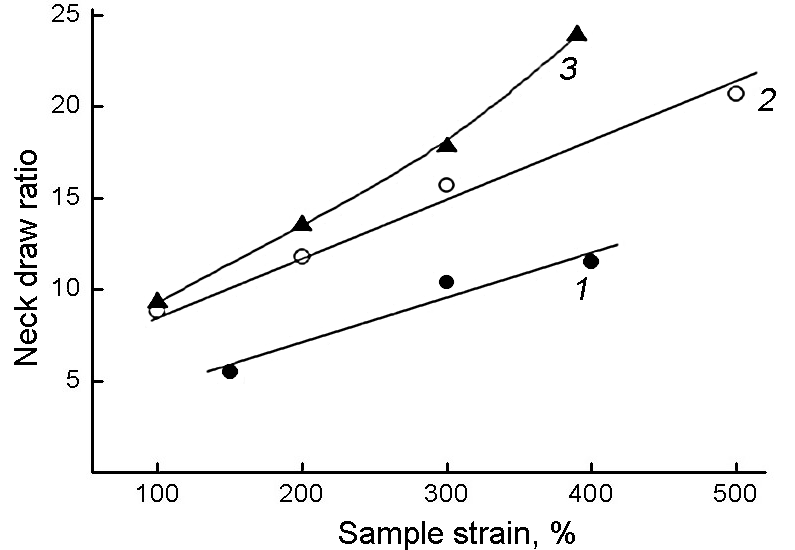
Figure 2. Dependence of the neck draw ratio of HDPE on the sample strain at 20 (1), 50 (2), and 70 (3) °C.

The introduction of fillers and elevated test temperatures can change the deformation behavior of the composites based on HDPE. A detailed analysis of the effect of temperature on the deformation character of the filled systems was carried out using the examples of specimens bearing 3 and 10 vol % of glass spheres. Figure 1b demonstrates the stress–strain curves of HDPE bearing 3 vol % of the filler. At to changes in the character of material tension.20 °C, this composite undergoes brittle failure at the initial step of the neck growth, which leads to a drastic drop in its relative elongation at break from 500% to 10%. A temperature rise by 10 °C changes the composite deformation behavior. Its tension is again accompanied by the appearance and growth of the neck. A further increase in the test temperature (T ≥ 30 °С) does not lead to changes in the character of material tension.

Figure 3a shows a surface micrograph of the sample of HDPE bearing 3 vol % of glass spheres in the region of the forming neck, which was fractured at 20 °C. It is obvious that fracture of this composite is caused by debonding of the filler particles and formation, cross-sectional growth, and integration of rhomboid pores in the region of the neck. The expansion angles of these critical defects at the pole are equal to 25–30° and those at the equator compose 140–160°. The size of the rhomboid pores in the direction of the sample tension reaches 0.5 mm. At 30 °С and above, the longitudinal splits or slit-like pores are formed instead of the rhomboid pores, which are caused by debonding of the filler from the matrix (Fig. 3b). The tension leads to the elongation of these defects, which can reach several hundreds of microns. At the same time, no cross-sectional growth is observed. This fact distinguishes them from the rhomboid pores and allows one to attribute them to innocuous defects. The material fractures upon the integration of several defects of this type in the neck; in this case, the sample looks like a bunch of ruptured fibers. The micrograph shows the oriented, fibrillated structure of the matrix polymer which resembles a fiber composite. It is apparent that this prevents the cross-sectional growth of pores.

Figure 3. Micrographs of the broken samples of the HDPE composites bearing 3 (a, b) and 10 (c, d, e) vol % of the filler.
The test temperatures were as follows: 20 (a, c), 30 (b, d), and 50 (e) °С.

The changes in the form of the defects that arise during the tension of the samples also predetermine the character of deformation and break of the HDPE composite bearing 10 vol % of the filler. Figure 1c shows the stress–strain curves of this composite. At 20 °С, the samples undergo brittle fracture, prior to reaching the yield stress. At 30 and 50 °С, the fracture occurs via the formation of a neck. Upon a further increase of the test temperature, filled HDPE deforms with the formation of a neck and fractures during its growth.

Figure 3 shows the micrographs of the fracture surfaces of the HDPE composite bearing 10 vol % of the filler. A brittle fracture at 20 °С is caused by the appearance of cross-sectional microsplits (Fig. 3с). Due to the break at low strains, the formation of pores on the sample surface is not observed. An increase in the temperature to 30 °С facilitates the variation of the resulting critical defects. The tension gives rise to rhomboid pores in the material (Fig. 3d). A further temperature increase leads to the next transformation of pores into innocuous split-like defects (Fig. 3e).

Hence, an increase in the test temperature suppresses the formation of innocuous defects in the composites of HDPE and glass spheres. This accounts for a change of the mechanism of composite fracture from brittle to ductile.

Figure 4 demonstrates the temperature dependences of the relative elongation at break for HDPE bearing different amounts of the filler. An increase in the filling degree facilitates a reduction in the deformability of the composite samples. The curves corresponding to HDPE with the concentration of glass spheres below 10 vol % show the maxima at Т = 50 °С, which presence is stipulated by the propensity of the matrix polymer for high-temperature embrittlement. At the filler content of 10 vol %, the break strain of the composite monotonously increases with a test temperature rise.

Figure 4. Temperature dependence of the relative elongation at break of the composites based on HDPE and glass spheres.
The filler contents were as follows: 3 (1), 5.5 (2), and 10 (3) vol %.

Figure 5 shows the dependences of strength characteristics of the materials (yield stress and tensile strength) on the content of glass spheres. An increase in the filler content in the polymer composition does not affect these characteristics of the material, while a temperature rise leads to their reduction.

Figure 5. Dependences of the yield stress (a) and tensile strength (b) of the composites based on HDPE on the content of glass spheres.
The test temperatures were as follows: 20 (1), 30 (2), 50 (3), 70 (4), and 90 °С (5).

It can be concluded that the content of the filler and the test temperature predetermine the shape of defects resulting in the composites during uniaxial tension and the character of material fracture (brittle or ductile). As a temperature increases, the defects transform from critical into innocuous, and the composite undergoes a brittle-to-ductile transition without changes in its composition.

It is obvious that the formation of rhomboid pores during the tension of materials based on a thermoplastic polymer is dictated by particle sizes of the filler in use. Earlier it was shown [11] that the shape of pores that are formed due to debonding of particles from a matrix during composite tension depends on the particle sizes. The critical particle size D_cr that leads to the appearance of innocuous pores is individual for each polymer and is defined by its fracture viscosity. At the low particle contents (V_f < 5 vol %), an oval-shaped pore formed in the sample neck transforms into a rhomboid one when its expansion reaches the value being equal to the critical expansion of a split (δ_cr) in the matrix polymer: D_cr = δ_cr(λ_d–1). For the HDPE grade under consideration, the critical split expansion at 20 °С composes 0.4 mm [12]. At λ = 10.4–11.5, the critical particle sizes are equal to 43–38 μM. In this case, the introduction of glass spheres with the diameter of 50 μM into the polymer must inevitably lead to the formation of rhomboid cracks, which was  observed in tests with the composites bearing 3 vol % of glass spheres at 20 °С.

The formation of cross-sectional cracks in the composite based on a polymer with the low deformation strength (i.e., the polymer that decomposes during neck propagation) with particle content V_f > 3 vol % is caused by the interaction of stress fields, which arise between closely located spheres and pores [13]. The maximum stresses are concentrated in the equatorial regions of the decomposed pores. During the tension of the composite, the stress is achieved in fine polymer layers, which is required for the plastic flow of the matrix polymer [14]. The material deformation is concentrated just in these layers. As a result, there are formed a variety of micronecks, which decompose upon further application of the tensile load. Consequently, in these zones the plastic flow of the matrix layers and their rupture lead, on the one hand, to a stress drop and, on the other hand, to an increase in the defect cross-sectional size. The crack changes the direction of its growth from longitudinal to cross-sectional relative to the sample tension axis.