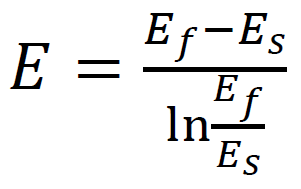2019 Volume 2 Issue 3

INEOS OPEN, 2019, 2 (3), 99–104  Journal of Nesmeyanov Institute of Organoelement Compounds of the Russian Academy of Sciences Download PDF DOI: 10.32931/io1914a

Theoretical Analysis of the Changes of Elasticity Modulus in Gradient Materials
 

  

A brief overview of the structures and properties of gradient-modulus polymeric materials is presented. Special attention is given to the analogs of gradient materials in biological objects and the possibility of their replication upon creation of materials for technical purposes. A main goal of this work is to develop a theoretical approach to evaluation of dependences of the elasticity modulus on the length or width of a gradient material. The linear and curvilinear dependences are demonstrated and the formulae and methods for their description are given. The suggested method is tested on poly(urethane-isocyanurate) networks obtained by the interaction of poly(propylene glycol) (PPG) and poly(tetramethylene glycol) (PTMG) with toluene 2,4-diisocyanate (2,4-TDI).

Key words: gradient-modulus polymeric materials, elasticity modulus, gradient composites, stress relaxation, poly(propylene glycol), poly(tetramethylene glycol), toluene 2,4-diisocyanate.

 

Introduction

Gradient-modulus polymeric materials were obtained for the first time in 1995 [1]. The syntheses and properties of carbofunctional organosilicon diols, macrodiisocyanates, and network polymers as well as the mechanical properties of gradient-modulus polymeric glasses based on these compounds were reported [2, 3]. The optically sensitive gradient-modulus materials were tested in a photoelastic method [4]. Subsequently, a detailed analysis of polyisocyanurate networks bearing low-molecular rubber residues as linear fragments between the cross-links showed that they are in a new physical state [5]. The latter has the following feature: the elasticity modulus can adopt any value between the modulus of an elastomer and the modulus of a glass and only slightly reduces upon a temperature rise, whereas for conventional polymers, an increase in the temperature and a transition from a glassy state to a rubbery one lead to a decrease in the elasticity modulus by an order of 0.4 of the initial value. The synthesis of gradient polymeric materials based on these networks was described in Ref. [6].

The idea of creation of gradient materials analogous to those in biological objects was used later in a series of works [7, 8]. Another example of the application of biomimetic principles in materials science is mussel protein fibers byssus. These fibers possess gradually changing mechanical properties along the length on passing from a soft region to a rigid one. Sea mussels use their fibers to attach to any substrate.

A simple approach to production of macroscopic lateral gradient polymeric materials in a centimeter scale was developed based on a polydimethylsiloxane system [7]. The gradient was realized using three syringe pumps that provided introduction of the precursors prone to thermal cross-linking. This afforded a fourfold change in the rigidities of solid and soft parts in the resulting gradient materials. The advances in the field of experimental methods for production of gradient materials using biomimetic principles and the methods for investigation of their structures and properties have been reviewed recently [8]. Claussen et al. focused on the problem of a reduction of stress concentration and an increase of fracture viscosity [9]. This was accomplished by the application of gradient materials. The authors succeeded in increasing the elasticity modulus of the rigid region of a gradient material up to 1300 MPa. A growth of the elasticity modulus was achieved by the application of new network polydimethylsiloxanes. It should be noted that even a higher increase in the elasticity modulus was reported in the earlier works of our research group [2, 3].

The methods for production of gradient materials were described in a series of Russian publications. Shock- and wear- resistant poly(urethane-isocyanurate) composite polymeric materials were described in Ref. [10]. The synthesis and mechanical properties of gradient composite poly(urethane-isocyanurate) polymeric materials based on oligo(oxytetramethylene glycol) were studied in detail [11, 12]. Further investigations on new polyisocyanurate networks based on toluene 2,4-diisocyanate and poly(oxytetramethylene glycol) afforded a lot of data not only on the mechanical properties, but also on the dependences of the elasticity modulus in a given direction of a gradient material sample [13]. A single-step protocol for the synthesis of network poly(urethane-isocyanurate) polymeric materials was developed [14, 15]. It was shown that this process combines precursor dosing and formation of a network of chemical bonds, which gives rise to gradient-modulus materials. The elasticity modulus gradually changed along the sample length from 3 MPa to 2000 MPa, i.e., there was observed a smooth transition from a rubber to a plastic within one and the same material without bonding, welding or other conventional techniques for coupling of materials with different moduli. At the same time, the effect of conditions for formation of a network polyurethane on the cross-linking degree and the mechanical properties was scrutinized [15]. The kinetic regularities of the formation of poly(epoxy-isocyanurate) networks were studied by NMR spectroscopy [16]. The latter appeared to be highly efficient not only for kinetic studies, but also for investigation of the chemical structures of the products obtained during the synthesis.

It should be noted that in a series of works, our research group suggested the modified method for production of gradient materials based on oligodiols and 2,4-TDI [17, 18]. According to this method, the reaction was carried out with an excess of the epoxy oligomer relative to the amount required for the formation of a catalytic system based on this oligomer and dimethylbenzylamine for the synthesis of a network polyisocyanurate. This modification allowed us to improve the mechanical properties of the resulting gradient materials. During investigation of the mechanical properties, particular attention was drawn to a dependence of the elasticity modulus on the length of the gradient material. It was shown that this dependence can be almost linear or curvilinear, depending on the method for precursor dosing and other factors. Therefore, the urgent tasks seem to be the prediction and description of the character of these dependences, which are the main goals of this work.

Experimentally the dependence of the elasticity modulus on the sample length is measured using microsamples, which are cut from a macrosample at regular intervals by the thickness. Figure 1 shows a scheme of a gradient material which is used to obtain the microsamples.

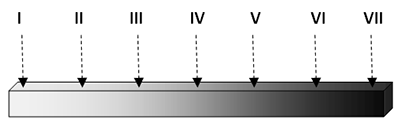
Figure 1. Scheme of a polymeric material; the gradient is directed along the sample. (I) midpoint of the zone with the minimum elasticity modulus,
(VII) midpoint of the zone with the maximum elasticity modulus.

Since the microsamples have small sizes, they are considered as single-modulus materials.

Theoretical analysis

Let us analyze the dependences of elasticity moduli during monoaxial tension or compression Е. A scheme of the gradient material loading upon compression is depicted in Fig. 2.

Let us select an infinitely small region at distance x from the sample edge (Fig. 2), at which the elasticity modulus is equal to E(x). At x = l₀, the elasticity modulus is designated as E_f, and at х = 0 the elasticity modulus is designated as Е_s.

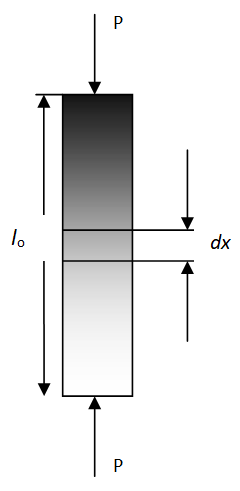
Figure 2. Scheme of the loading of a gradient material.

The strain can be calculated by the equation

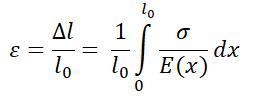(1)

In the case of a linear gradient, the elasticity modulus changes according to the following law

E(x) = Es+ αx

(2)

where x is the distance from the sample edge,

(3)

Then

(4)

In the case of a stepwise gradient

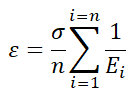(5)

where n is the number of steps, E_i is the elasticity modulus of the material at each step.

Since E = σ/ε, we obtain

(6)

In the case of a stepwise gradient

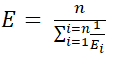(7)

Let us analyze the dependences of the elasticity modulus on the sample length in the case of different types of a gradient.

Linear dependence

The elasticity modulus of a gradient material is defined by formula (2).

Parabolic dependence

E = Es + 2Вx + Сх2

(8)

In this case, the shear modulus of a gradient material is defined as follows

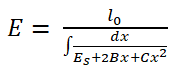(9)

where х is the distance from the elastic edge of the material.

The value of a denominator in relation (9) can be found using the following equations

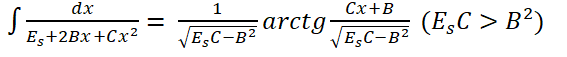(10)

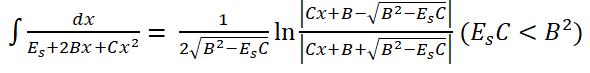(11)

To estimate the changes of elasticity modulus along the sample of a gradient material, a special computer program was developed that has the following main principle. At the first step, the elasticity modulus of a gradient material is calculated on the assumption of a linear dependence of the modulus on the sample length. The calculation is carried out according to formula (6). If the calculated value of the modulus does not coincide with the experimental one, the modulus gradient is curvilinear. Then, the calculation is carried out according to formula (8) with the given step of variation of the elasticity modulus in the middle part of the sample. Coefficients 2B and C are chosen using the following procedure. If the value calculated by formula (6) is higher than the experimental one, then an average value of the modulus is found first, which is equal to (E_s+E_f)/2 at x = l₀/2, and then a series of E' values lower than (E_s+E_f)/2 at x = l₀/2 are introduced. Based on formula (8), pairs of equations are formed for the following cases: x = l₀/2 and x = l₀. The solution of each pair of the equations gives the values of coefficients 2В and С. Subsequently, the values of the moduli are calculated by formula (9), taking into account relation (10) or (11). Let us remind that this procedure is valid for the case when the value calculated by formula (6) is higher than the experimental one.

If the value calculated by formula (6) is lower than the experimental one, then an average value of the modulus is found first, which is equal to (E_s+E_f)/2 at x = l₀/2, then a series of E values higher than (E_s+E_f)/2 at x= l₀/2 are introduced. Based on formula (8), pairs of equations are formed for the following cases: x = l₀/2 and x = l₀. The solution of each pair of the equations gives the values of coefficients 2В and С. Subsequently, the values of moduli are calculated by formula (9), taking into account relation (10) or (11). Finally, coefficients 2В and С are found that correspond to the case when the calculated value of the modulus is equal to the experimental one.

Figure 3 depicts the dependence of shear modulus E on the temperature for a sample based on PTMG with the gradient arrangement along it (sintepon filler). The related samples were obtained earlier [15, 17]. Figure 3 shows also the calculated dependence at the linear modulus gradient. It is obvious that the calculated dependence (curve 2) lies somewhat higher than the experimental one (curve 1).

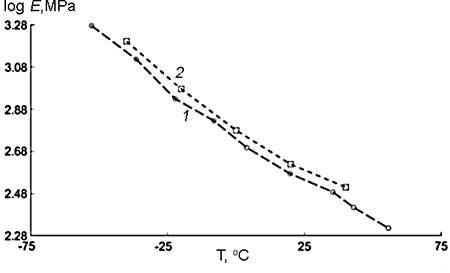
Figure. 3. Dependences of storage modulus E on the temperature for a sample based on PTMG with the gradient arrangement along it (sintepon filler):
(1) experimental curve, (2) calculated curve for the linear modulus gradient.

Coefficients 2В and C are used to construct the graphs for dependences of the elasticity modulus on the sample length according to formula (8) at all the temperatures explored (Fig. 4). Figure 4 shows that the modulus gradient in all the samples is parabolic but close to the linear dependence. It is interesting to note that the character of the modulus gradient slightly changes depending on the temperature. This is connected with the peculiarities of the temperature dependences of elasticity moduli of single-modulus materials.

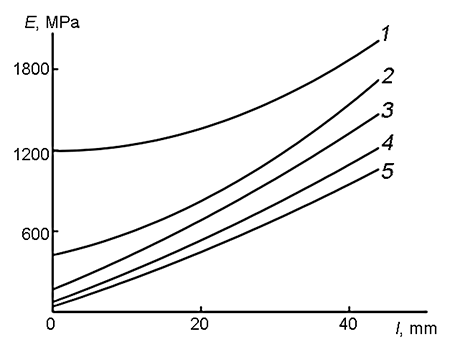
Figure 4. Dependences of the dynamic modulus on the sample length. A composite derived from PTMG with the gradient arrangement along the sample (sintepon filler). Test temperatures: –40 °С (1), –20 °С (2), 0 °С (3), 20 °С (4), 40 °С (5).

From Fig. 4 it is obvious that at the low temperature (–40 °С) the modulus gradient is rather curvilinear, especially in the initial region of the curve. This can be connected with the fact that at low temperatures the shear moduli of both gradient and single-modulus materials, located at the butt ends of the gradient sample, are close to each other. At the other temperatures, the curvilinearity is only weakly expressed and the dependences of the shear modulus on the sample length are almost linear.

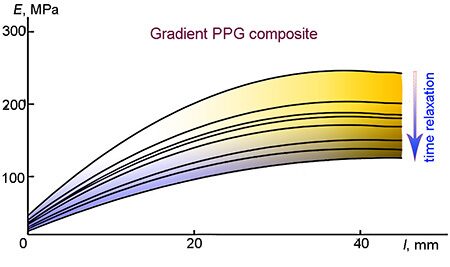
For a sample based on PPG, the analogous dependences are observed (Fig. 5). A difference is that the flexure of the modulus dependence on the sample length changes its sign in the region of relatively high temperatures. In general, the resulting gradient materials are of high quality, which is reflected in the fact that in one and the same sample the shear modulus changes smoothly by the very high value (from 5 to 26 times).

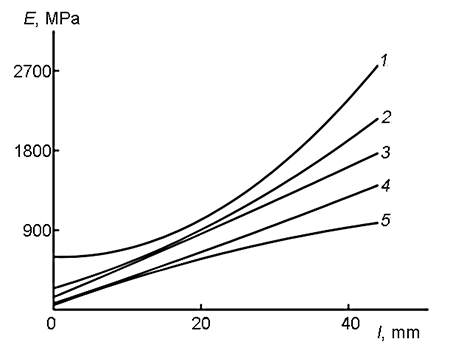
Figure 5. Dependences of the dynamic modulus on the sample length. A composite derived from PPG with the gradient arrangement along the sample (sintepon filler). Test temperatures: –20 °С (1), 0 °С (2), 20 °С (3), 40 °С (4), 60 °С (5).

For the detailed evaluation of the elasticity modulus, the stress relaxation curves were measured at different temperatures for single-modulus and gradient materials obtained based on PTMG and PPG. The stress relaxation curves for the gradient material based on PTMG are demonstrated in Fig. 6.

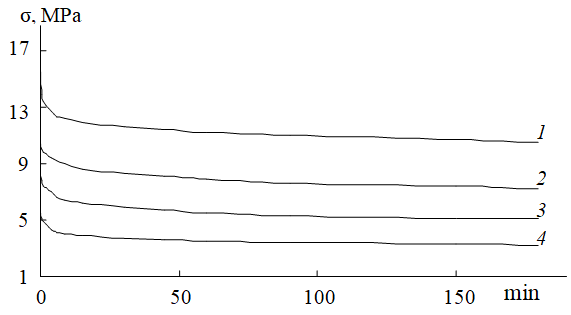
Figure 6. Stress relaxation curves for the gradient sample based on PTMG. Test temperatures: 20 °С (1), 65 °С (2), 105 °С (3), 165 °С (4).

It is obvious that the stress at the initial moment reduces rather rapidly, but then its decline drastically retards and the stress, which is required to retain a constant strain, almost does not change. It should be noted that the total range of the stress drop for 180 min is small and reduces with a temperature rise.

The values of Е_r measured at different durations of the relaxation process are listed in Table 1. Based on these data, the values of parameters 2В and С from equation (8) were calculated using the above-described computation program.

The resulting parameters were used to construct the dependences of elasticity modulus on the sample length (for example, see Figs. 7 and 8).

Table 1. Parameters of the gradient material based on PTMG (sintepon filler, gradient along the material length)

Relax. duration, min	Egrad.mater., MPa		2B		С
	20 °С	165 °С	20 °C	165 °С	20 °С	165 °С
0	478.2	162.4	63.579	19.77	–0.96	–0.248
1	388.2	145.7	49.133	18.865	–0.685	–0.275
4	347.8	136.7	42.407	18.041	–0.554	–0.266
6	337.5	133.4	40.931	17.641	–0.53	–0.261
15	322.7	126.5	38.957	16.951	–0.498	–0.252
45	307.9	114.8	37.185	15.426	–0.476	–0.227
90	296.0	103.6	35.731	13.876	–0.456	–0.202
180	284.7	89.0	34.407	11.709	–0.443	–0.164

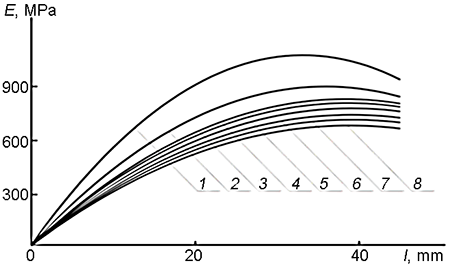
Figure 7. Dependences of the elasticity modulus on the length at different durations of the relaxation process: 0 (1), 1 (2), 4 (3), 6 (4), 15 (5), 45 (6), 90 (7), and 180 (8) min. A composite derived from PTMG with the gradient arrangement along the sample; sintepon filler; temperature 20 °С.

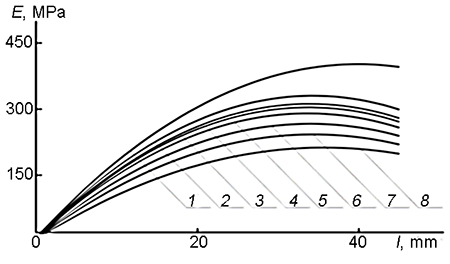
Figure 8. Dependences of the elasticity modulus on the length at different durations of the relaxation process: 0 (1), 1 (2), 4 (3), 6 (4), 15 (5), 45 (6), 90 (7), and 180 (8) min. A composite derived from PTMG with the gradient arrangement along the sample; sintepon filler; temperature 165 °С.

These dependences were obtained at 20 and 165 °С. The analogous dependences were obtained also at other temperatures for the samples of various chemical structures. Naturally, the dependences at different temperatures slightly differ. In the presented cases, they are not ideally linear and have clear flexures. It should be noted that during the production of gradient materials, it is possible to change the gradient shape and even to achieve the highest elasticity modulus inside the sample rather than at its edge. All this offers ample opportunities for the formation of an elasticity modulus gradient with a transition from an elastic material to a rigid one without any interface.

The curves of stress relaxation for the gradient materials based on PPG measured at different temperatures are depicted in Fig. 9.

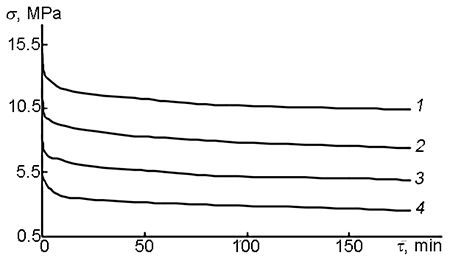
Figure 9. Stress relaxation curves for the composite derived from PPG with the gradient arrangement along the sample length.
Test temperatures: 20 (1), 65 (2), 105 (3), 165 °С (4).

The values of Е_r for the materials based on PPG at different durations of the relaxation process are listed in Table 2.

Table 2. Parameters of the gradient material based on PPG (sintepon filler)

Relax. duration, min	Egrad.mater., MPa		2B		C
	20 °С	165 °С	20 °С	165 °С	20 °С	165 °С
0	541.2	159.4	30.981	10.518	–0.248	–0.138
1	442.0	132.7	24.959	8.489	–0.177	–0.11
4	420.6	122.8	25.409	7.99	–0.222	–0.105
6	410.9	119.0	24.767	7.633	–0.216	–0.099
15	393.5	111.86	24.545	7.195	–0.227	–0.094
45	374.3	96.6	24.629	5.894	–0.253	–0.072
90	357.0	89.42	23.133	5.531	–0.225	–0.069
180	346.3	78.5	22.051	4.632	–0.206	–0.053

These dependences were used to calculate parameters 2В and С from equation (8) and to construct the dependences of the elasticity modulus on the sample length. Figures 10 and 11 show that the materials based on PPG feature more linear gradients of the elasticity modulus than those based on PTMG.

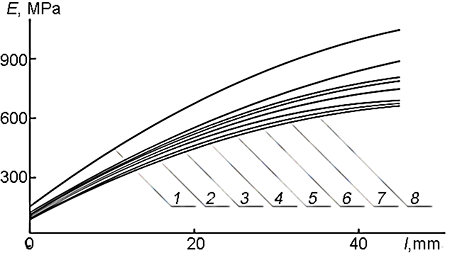
Figure 10. Dependences of the elasticity modulus on the length at different durations of the relaxation process: 0 (1), 1 (2), 4 (3), 6 (4), 15 (5), 45 (6), 90 (7), and 180 (8) min. A composite derived from PPG with the gradient arrangement along the sample; sintepon filler; temperature 20 °С.

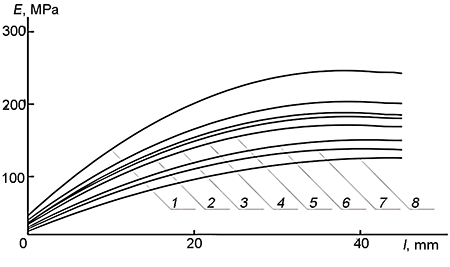
Figure 11. Dependences of the elasticity modulus on the length at different durations of the relaxation process: 0 (1), 1 (2), 4 (3), 6 (4), 15 (5), 45 (6), 90 (7), and 180 (8) min. A composite derived from PPG with the gradient arrangement along the sample; sintepon filler; temperature 165 °С.

The dependences obtained for the composites based on PPG possess the lower flexure degree than those based on PTMG, especially at low temperatures.

The physical interpretation of parameters 2B and C of the parabolic distribution of the elasticity modulus is connected with the generalized equation of the theory of high elasticity suggested in papers [19–22]. One of the forms of this equation can be presented as follows

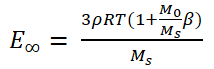(12)

where ρ is the polymer density, R is the universal gas constant, T is the absolute temperature, M₀ is the molar mass of a repeating unit, M_s is the molar mass of a mechanical segment of the macromolecule (i.e., the molar mass which exceeding leads to the appearance of the rubbery state), β is the volume of a domain which serves as a network cross-link.

The network cross-link represents a group of atoms that includes a branching point and the adjacent atoms, which are chemically bound to this atom, along with the closest substituents. The cross-link point can also be a domain formed by the aggregates of molecular cross-links.

Recently we performed a detailed analysis of the situation when an elastomeric matrix contains a definite amount of solid glassy particles, which play the role of domains [23]. For example, for a mixture of PMMA with 1,4-polybutadiene at the content of PMMA of 20%, the elasticity modulus is determined by the following relation

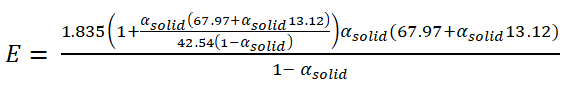(13)

Relation (13) is valid for the domain volume β = 1000 ų.

After a short description of the modified theory of high elasticity, let us return to the interpretation of parameters 2B and C. As it follows from Table 1, for the gradient material based on PTMG, at the test temperature of 20 °С and the relaxation duration of 1 min parameter 2B changes by 22.7% and at 165 °С and the same relaxation duration it changes by 4.6%. Similar analyses at other temperatures and relaxation durations result in the same relationship. At the relaxation duration of 180 min and the temperature of 20 °С, parameter 2B changes by 46%, while at 165 °С and the same relaxation duration it changes by 41%. This character of changes stems from the fact that the generalized equation of the high elasticity theory uses an equilibrium high elasticity modulus. Therefore, the longer the relaxation process duration, the closer the elasticity modulus to the equilibrium value. This explains the character of changes of parameters 2B and C with an increase in the duration of the stress relaxation process. It is natural that the character of these changes depends on the chemical structure of a material and differs for the materials based on PPG and PTMG. As for the temperature effect, theoretically the high elasticity modulus must increase with a temperature rise, but since the material contains elastic inclusions in the form of domains, the elasticity modulus must reduce. All this is taken into account in the theory described in Ref. [23] and leads to the fact that at 20 °C the value of constant C reduces by 54% with the prolongation of the stress relaxation duration from 0 to 180 min, and at 165 °С—by 34%. All this is valid for the gradient material based on PTMG. For the material based on PPG, these changes compose 17% and 61.5%. A small change of constant C for the material based on PPG is connected with the fact that the chains of this polymer, which join the cross-links, are shorter than the analogous chains in PTMG. Therefore, at relatively low temperatures, the role of solid domains is more expressed. At the elevated temperatures, these domains soften and the changes in constants C level.

Conclusions

The performed analysis show that short tests with gradient materials, which are aimed to measure the elasticity modulus in the middle part of a sample, allow for the prediction of a dependence of the elasticity modulus on the sample length. This can afford both linear and curvilinear dependences. The character of a flexure of these dependences is defined by the chemical structure of a network polymer, the filler type, and the temperature. The computation method was tested on the gradient materials derived from PPG and PTMG by the interaction with 2,4-TDI. The high rate of convergence between the calculated and experimental data was achieved.

Acknowledgements

This work was supported by the Ministry of Science and Higher Education of the Russian Federation.

References

1. A. A. Askadskii, L. M. Goleneva, K. A. Bychko, Vysokomol. Soedin., Ser. A, 1995, 37, 829–841.
2. A. A. Askadskii, G. V. Surov, V. A. Pankratov, Ts. M. Frenkel', L. I. Makarova, A. A. Zhdanov, I. V. Blagodatskikh, A. V. Pastukhov, Vysokomol. Soedin., Ser. A, 1990, 32, 1528–1534.
3. A. A. Askadskii, G. V. Surov, V. A. Pankratov, Ts. M. Frenkel', A. A. Zhdanov, L. I. Makarova, A. S. Marshalkovich, L. G. Radchenko, Vysokomol. Soedin., Ser. A, 1990, 32, 1517–1527.
4. A. A. Askadskii, G. V. Surov, A. S. Marshalkovich, V. V. Dvalishvili, V. A. Pankratov, Ts. M. Frenkel', Mech. Compos. Mater., 1991, 27, 1–5. DOI: 10.1007/BF00630709
5. A. A. Askadskii, A. E. Shvorak, T. M. Frenkel, T. M. Babtschinitzer, C. A. Bychko, O. V. Kovriga, V. A. Pankratov, A. V. Rajulu, J. Appl. Polym. Sci., 1995, 55, 1173–1183. DOI: 10.1002/app.1995.070550804
6. A. Askadskii, L. Goleneva, Macromol. Symp., 1996, 106, 9–18. DOI: 10.1002/masy.19961060104
7. K. U. Claussen, R. Giesa, T. Scheibel, H.-W. Schmidt, Macromol. Rapid Commun., 2012, 33, 206−211. DOI: 10.1002/marc.201100620
8. K. U. Claussen, T. Scheibel, H.-W. Schmidt, R. Giesa, Macromol. Mater. Eng., 2012, 297, 938–957. DOI: 10.1002/mame.201200032
9. K. U. Claussen, R. Giesa, H.-W. Schmidt, Polymer, 2014, 55, 29–38. DOI: 10.1016/j.polymer.2013.11.018
10. M. D. Petunova, L. V. Luchkina, A. A. Askadskii, Perspekt. Mater., 2007, 3, 470–471.
11. M. D. Petunova, L. V. Luchkina, A. A. Askadskii, O. V. Afonicheva, Perspekt. Mater., 2008, 1, 1–5.
12. M. D. Petunova, L. V. Luchkina, A. A. Askadskii, V. V. Kazantseva, O. V. Afonicheva, Plast. Massy, 2008, 2, 22–25.
13. M. D. Petunova, L. V. Luchkina, A. A. Askadskii, O. V. Kovriga, Polym. Sci., Ser. A., 2009, 51, 542–549. DOI: 10.1134/S0965545X09050083
14. M. D. Petunova, A. A. Askadskii, L. V. Luchkina, L. M. Goleneva, O. V. Kovriga, Plast. Massy, 2010, 1, 30–38.
15. M. D. Petunova, L. M. Goleneva, A. A. Askadskii, O. V. Afonicheva, Konstr. Kompoz. Mater., 2010, 1, 45–53.
16. E. S. Afanas'ev, M. D. Petunova, L. M. Goleneva, A. A. Askadskii, T. P. Klimova, T. A. Babushkina, Polymer Sci., Ser. A., 2010, 52, 1318–1326. DOI: 10.1134/S0965545X10120102
17. M. D. Petunova, A. A. Askadskii, L. M. Goleneva, M. G. Ezernitskaya, V. V. Kazantseva, G. G. Nikiforova, Konstr. Kompoz. Mater., 2011, 3, 22–27.
18. M. D. Petunova, A. A. Askadskii, L. M. Goleneva, G. G. Nikiforova, L. A. Vasserman, O. V. Kovriga, V. A. Markov, Polym. Sci., Ser. A., 2011, 53, 984–992. DOI: 10.1134/S0965545X11100105
19. A. A. Askadskii, Computational Materials Science of Polymers, Cambridge Int. Sci. Publ., Cambridge, 2003.
20. A. A. Askadskii, A. R. Khokhlov, Introduction to Physical Chemistry of Polymers, Nauchnyi Mir, Moscow, 2009 [in Russian].
21. A. A. Askadskii, V. I. Kondrashchenko, Computational Materials Science of Polymers, vol. 1, Atomic-Molecular Level, Nauchnyi Mir, Moscow, 1999 [in Russian].
22. A. A. Askadskii, M. N. Popova, V. I. Kondrashchenko, Physical Chemistry of Polymeric Materials and Methods for Their Investigation, ASV, Moscow, 2015 [in Russian].
23. A. A. Askadskii, T. A. Matseevich, M. N. Popova, Secondary Polymeric Materials. Mechanical and Barrier Properties, Plasticization, Blends and Nanocomposites, ASV, Moscow, 2017 [in Russian].